Korszerű geodéziai adatfeldolgozás
Kulcsár Attila
Nyugat-Magyarországi Egyetem
Térinformatika Tanszék
8000 Székesfehérvár, Pirosalma 1-3
Tel/fax: (22) 348 271
E-mail: a.kulcsar@geo.info.hu
A korszerű mérőállomások megjelenésével a geodéziai munkákban a felmért adatok feldolgozása egyszerűsödött a műszerekbe beépített feldolgozó rutinok segítségével. De ez nem minden esetben megfelelő. A nagytömegű, azonos típusú adatfeldolgozáshoz – például tájékozás, poláris pontszámítás – hatékony, de az összetettebb számítási műveleteket nagyon nehézkesen, vagy nem is lehet mindig megoldani velük.
Napjainkban tehát még mindig szükség van egy feldolgozó programra, amivel minden fajta számítást gyorsan, egyszerűen, lehetőleg minél hatékonyabb munkával lehet elkészíteni.
Milyen programra van akkor szükségünk?
Alapvető feltétel, hogy egy mérőállomással mért adatokat be lehessen olvasni vele, így a mérési adatok bevitele gyors, és elméletileg hibamentes.
A további feldolgozás általában a jól bevált kérdezz-felelek módszeren alapul, ahol ki lehet választani a megfelelő mérési eredményeket, a kívánt számítási módszert, és ez alapján a program kiszámolja az eredményeket. Ennek egy felhasználó „barátabb” megoldása, ha grafikusan tudjuk az adatokat, módszereket kiválasztani.
Az ideális eset az volna, ha a mérési adatokat a feldolgozó program automatikusan – lehetőleg semmilyen, vagy nagyon minimális beavatkozással tudná kiszámítani.
A továbbiakban szeretnék egy olyan feldolgozási módszert ismertetni, amely a hagyományos feldolgozás minden előnyét kihasználja, és megpróbálja az automatikus feldolgozást minél jobban megközelíteni.
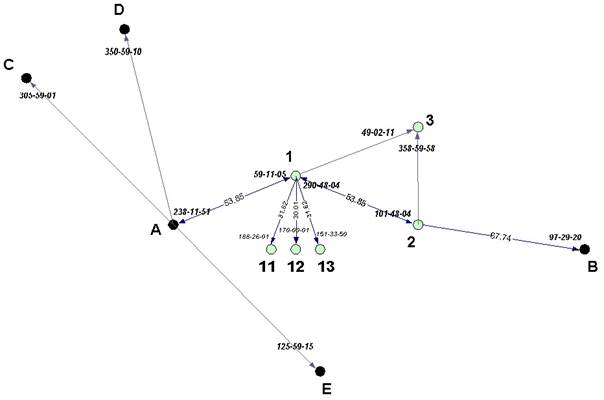
A geodéziai számítások logikai lépéseit és gyakorlati végrehajtását már a középiskolában, a főiskolán, vagy az egyetemen megtanulhattuk. Ezek ismeretében nézzük meg az alábbi – kitalált - felmérés ábráját:

Első ránézésre megállapítható, hogy az A és B pontok között egy sokszögvonalat vezettünk, az 1-es pontról polárisan meghatároztuk a 11-13. pontokat, illetve az 1-es és 2-es pontok segítségével meghatároztuk a 3-as pontot tájékozó irányok segítségével.
A feldolgozás során az alábbi lépéseket kell végrehajtanunk:
|
1 |
Koordináták megadása |
A ismert pontok koordinátáit meg kell határozni.
|
2 |
Tájékozás végrehajtása |
Az A ponton meg kell határozni a tájékozási szöget.
|
3 |
Sokszögvonal számítása |
Az A és B pontok között ki kell számolni a sokszögvonalat, így meghatározhatjuk az 1 és 2 pontokat.
|
4 |
Pontmeghatározás (1-ről) |
Az 1-es ponton meg kell határozni a tájékozási szöget, majd polárisan ki lehet számítani a 11-13. pontokat.
|
5 |
Pontmeghatározás (3-ast) |
Az 2-es ponton meg kell határozni a tájékozási szöget, majd az 1-es pont bevonásával tájékozott irányos előmetszéssel ki lehet számítani a 3. pontokat.
A feldolgozás kódolásának elvi alapjait 1989-90-ben fejlesztettem ki, gyakorlati megvalósítása 1991-ben készült el GeoCalc v1.0 néven. Nézzük meg az előző felmérés adatainak kódolását:
|
1 |
Koordináták megadása |
|
|
K_ A 80 110 B 247 100 C 20 170 D 80 190 E 140 50 ;; |
A feldolgozás során az ismert pontok koordinátái a memóriában tárolva lesz, később bármikor felhasználható. |
|
2 |
Tájékozás végrehajtása |
|
|
TJ A C 305.5901 D 350.5910 E 125.5915 ;; |
A tárolt adatok (koordináta) alapján a tájékozás során az A álláspont tájékozási szöge a memóriában tárolva lesz, később bármikor felhasználható. |
|
3 |
Sokszögvonal számítása |
|
|
SV A 59.1105 53.85 B 1 238.1151 101.4804 53.85 2 290.4804 97.2920 67.74 ;; |
A tárolt adatok (koordináta, tájékozási szög) alapján a számítás után a sokszögpontok (1, 2) koordinátái eltárolódnak. |
|
4 |
Pontmeghatározás (1-ről) |
|
|
TJ 1 A 238.1151 2 101.4804 ;; PO 1 11 188.2601 31.62 12 170.0001 30.01 13 151.3350 31.62 ;; |
A tárolt adatok (koordináta) alapján az 1-es pont tájékozási szöge a memóriában tárolva lesz
A tárolt adatok (koordináta, tájékozási szög) alapján a poláris számítás után a részletpontok (11-13) koordinátái eltárolódnak. |
|
5 |
Pontmeghatározás (3-ast) |
|
|
TJ 2 1 290.4804 B 97.2920 ;; ET 3 1 49.0211 2 358.5958 ;; |
A tárolt adatok (koordináta) alapján a 2-es pont tájékozási szöge a memóriában tárolva lesz
A tárolt adatok (koordináta, tájékozási szög) alapján a tájékozott irányos előmetszés számítása után a 3-as pont koordinátái eltárolódik. |
A fent bemutatott kódolást ha összesítjük, akkor az alábbi eredmény születik:
K_
A 80 110
B 247 100
C 20 170
D 80 190
E 140 50
;;
TJ
A
C 305.5901
D 350.5910
E 125.5915
;;
SV
A 59.1105 53.85 B
1 238.1151 101.4804 53.85
2 290.4804 97.2920 67.74
;;
TJ
1
A 238.1151
2 101.4804
;;
PO
1
11 188.2601 31.62
12 170.0001 30.01
13 151.3350 31.62
;;
TJ
2
1 290.4804
B 97.2920
;;
ET
3
1 49.0211
2 358.5958
;;
Ha ezt feldolgozzuk egy olyan programmal, ami érti ezt a kódolást, akkor a következő eredményt kapjuk:
Felhasznált koordináták :
Pontszám Y X M Kód
A 80.000 110.000 0.000 0
B 247.000 100.000 0.000 0
C 20.000 170.000 0.000 0
D 80.000 190.000 0.000 0
E 140.000 50.000 0.000 0
Végleges tájékozás [A]
Pontszám l de t zi e" h H
---------------------------------------------------------------
A Zk = 9.0051
---------------------------------------------------------------
C 305.5901 315.0000 84.853 9.0059 8 61 69
D 350.5910 0.0000 80.000 9.0050 -1 69 71
E 125.5915 135.0000 84.853 9.0045 -6 62 69
---------------------------------------------------------------
Egyszeresen tájékozott sokszögvonal számítása
Pontszám Lh D T DYjav DXjav dy dx
Le Ejav" DYi DXi Y X
-------------------------------------------------------------------------------
A 80.000 110.000
59.1105 68.1156 0.002 0.001 50.000 20.000
1 238.1151 0.00 53.850 49.999 19.999 130.000 130.000
101.4804
223.3614 111.4809 0.002 0.001 50.000 -20.000
2 290.4804 0.00 53.850 49.998 -20.000 180.000 110.000
97.2920
166.4117 98.2925 0.002 0.001 67.000 -10.000
B 97.2920 67.740 66.998 -10.001 247.000 100.000
-------------------------------------------------------------------------------
0.0000 175.440 166.99 -10.00 167.00 -10.00
0.006 0.002
d= 0.006 D= 93.2536
Végleges tájékozás [1]
Pontszám l de t zi e" h H
---------------------------------------------------------------
1 Zk = 10.0002
---------------------------------------------------------------
A 238.1151 248.1156 53.852 10.0005 2 84 86
2 101.4804 111.4804 53.851 10.0000 -2 84 86
---------------------------------------------------------------
Polárisan bemért pont(ok) számítása [1]
Pontszám Y X Li T Zi/d dM M
------------------------------------------------------------------------------------
1 130.000 130.000 10.0002 0.000
------------------------------------------------------------------------------------
11 120.002 100.002 188.2601 31.620 198.2603 0.000 0.000
12 130.000 99.990 170.0001 30.010 180.0003 0.000 0.000
13 140.000 100.003 151.3350 31.620 161.3352 0.000 0.000
Végleges tájékozás [2]
Pontszám l de t zi e" h H
---------------------------------------------------------------
2 Zk = 1.0001
---------------------------------------------------------------
1 290.4804 291.4804 53.851 1.0000 -1 85 86
B 97.2920 98.2921 67.742 1.0001 1 76 77
---------------------------------------------------------------
Előmetszés számítása tájékozott irányértékekkel
Pontszám Y X d
-----------------------------------------------
1 130.000 130.000 59.0213
2 180.000 110.000 359.5959
-----------------------------------------------
3 180.000 159.999
-----------------------------------------------
Az előzőekben ismertetett kódolás jellemzői:
Mind a bemenő, mind a kimenő adatokat egy szöveges állományban lehet tárolni, így könnyedén megoldható a különböző adatrögzítő formátumok beolvasása, és az eredmény igény szerinti nyomtatása.
· könnyű, gyors adatjavítás
Elmarad a „kérdezz-felelek” módszer, egyedileg és nagyon hatékonyan lehet a feldolgozási lépéseket meghatározni.
E kódolási eljárás alapján történő számítás gyakorlati megvalósításáról a http://www.geocalc.hu honlapon lehet több információt olvasni.