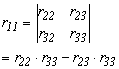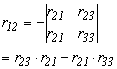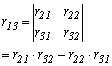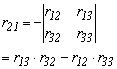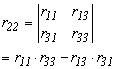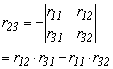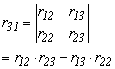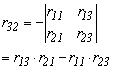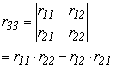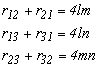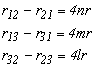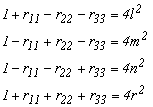forgatás

Csepregi Szabolcs^*

A dolgozatban a térbeli forgatással foglalkozunk. A gyakorlatban ez a legfontosabb térbeli transzformációs eljárás. A forgatómátrix tulajdonságainak bemutatása után. Külön fejezetben foglalkozunk azok felírásának lehetőségeivel, 8 különböző forgató mátrixot írunk fel. Ezek paramétereinek kapcsolatát is vizsgáljuk. Többféle lehetőséget mutatunk be a paraméterek meghatározására a forgatási mátrixból. Az utolsó két fejezetben a forgatómátrix kiegyenlítéssel történő meghatározását mutatjuk be, az ortogonalitási kényszerfeltételek felírásával és a kis elfordulások, paraméterváltozások bevezetésével alkalmazott iterációs eljárásokat ismertetjük. A dolgozatban szereplő számítási eljárásokat számpélda kapcsán is bemutatjuk. A dolgozat nem lezárt. További kiegyenlítési megoldások is vannak részben készen. Ezekről egy későbbi tanulmányban szeretnénk beszámolni.

Bevezetés

A forgatással foglalkozó jelen dolgozatban, 6 fejezetben mutatjuk be a kapcsolatos ismereteket.

Az első fejezetben adjuk a forgató mátrix tulajdonságait. Itt mutatjuk be az alkalmazott jelöléseket, melyeket az egész dolgozatban alkalmazni fogunk. Összefoglaljuk a későbbiekben részletesen bemutatandó forgató mátrixokat.

A második fejezet a forgató mátrix különböző felírási lehetőségeit tárgyalja. Tárgyaljuk a térbeli tengely körüli forgatást, az átlón kívüli elemek különbségei alapján felírható forgató mátrixot, ferdén szimmetrikus mátrixból felírható forgató mátrixot, a Rodriques mátrixot, Euler szimmetrikus paramétereit, a koordináta tengely körüli forgatások esetében a három különböző tengely körüli és a két különböző tengely körüli forgatást mutatjuk be. Ezután az Euler hat szögparaméterével felírható mátrixszot, és a három átlón kívüli elem paraméterként való használatát mutatjuk be. Végül a kis szögekkel és más kis paraméterváltozásokkal végzett forgatást mutatjuk be.

A harmadik fejezetben a különböző forgatási paraméterek kapcsolatával foglalkozunk.

A negyedik fejezet, egy adott forgatási mátrixból, a különböző paraméterek meghatározásával foglalkozik.

Az ötödik fejezetben mutatjuk be a forgatási mátrix kiegyenlítéssel történő számítását. Bemutatjuk a forgatómátrix meghatározását kényszer feltételi egyenletek felírásával, és a paraméterek kis változásainak segítségével való megoldását.

A hatodik fejezetben mintapéldákat adunk az elmondottakra és az iterációs megoldások tapasztalatait ismertetjük.

A dolgozat csak a kutatások első részét mutatja be, a további eredményekről a folytatásban szeretnénk beszámolni.

Egy forgatásról szóló dolgozatban meg kell emlékezni Euler Leonhard svájci matematikusról is.

Leonhard Euler, 1707-ben, Bázelben született. Apja szegény református lelkész volt. Johann Bernoulli ismerte fel matematikai tehetségét. Ott kötött barátságot a két Bernoulli fiúval, Nicolausszal és Daniellel. Az egyetemet kiváló eredménnyel végezte de nem kapott állást. A Bernoulli testvérek segítségével kerül a szentpétervári akadémiára 1727-ben. Kezdetben az élettant tanított, de csakhamar átkerült a matematikai fizikai tanszékre és ennek lett később a tanára. Közben Oroszország térképeit is szerkeszti. Valószínűleg ebbe a munkába vakul meg egyik szemére 31 éves korára, 59 évesen már majdnem teljesen vak. Ez időben munkáit tanítványainak és inasának diktálta. 1741-től Berlinben dolgozik az akadémián, a szentpétervári akadémiának továbbra is tiszteletbeli tanára maradt. Katalin cárnő továbbra is fizetést adott neki, és az ő hívására, 1766-ban ismét Szentpétervárra ment az akadémiára. 886 könyve és tanulmánya jelent meg. A matematika majd minden ágával foglalkozott. 1783-ban halt meg.

1. A forgatási mátrix

1.1. Bevezetés

A leggyakrabban használt transzformáció a térbeli forgatás. Geodéziai gyakorlatban igen széles körben kerül alkalmazásra.

A lineáris transzformációk egyenletét az alábbi formában szoktuk felírni

ahol az X koordináta vektor az első rendszerbeli koordinátákat foglalja magába. Az Y vektor a második rendszerbeli koordinátákat tartalmazza. Az T vektor az eltolás (transzláció) paramétereit foglalja magába. Az R mátrix a transzformáció mátrixa.

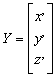
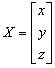
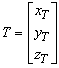
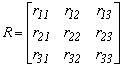
Az R mátrix tulajdonságaitól függ, hogy a transzformáció milyen lesz. Ha az R mátrix tetszőleges, akkor a leképzés térbeli affin transzformáció lesz. A transzformációs egyenletet transzponált formában is felírhatjuk

Ezt az egyenletet elsősorban az R mátrix kiegyenlítéssel történő meghatározásánál fogjuk használni.

A két különböző koordináta halmaz egymásba transzformálása két féleképpen fogható fel.

Az első esetben a két koordináta halmazt két különböző koordináta rendszerben lévőnek fogjuk fel, ekkor a két koordináta rendszer egymáshoz képest eltolt és elforgatott helyzetben van. A transzformáció paraméterei az eltolás és elforgatás. Síkban ez két eltolást és egy elforgatást jelent. Térben három eltolási paraméter van és három forgatási paraméter.

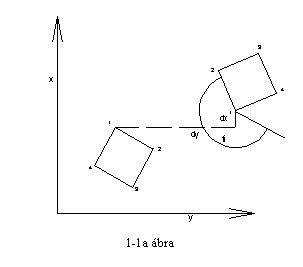
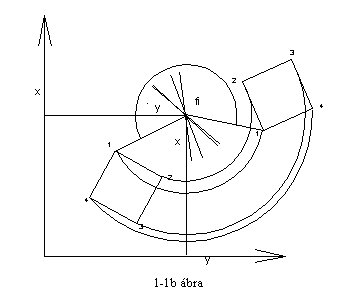
A forgatást úgy is felfoghatjuk, hogy az ugyan azt a két koordináta halmazt egy koordináta rendszerben lévőnek fogjuk fel, melyek különböző helyen vannak. A két halmaz kapcsolatát úgy teremtjük meg, hogy síkban megadjuk egy pont koordinátáját és megadjuk az elfordulás szögét. Térben ez egy forgástengely megadását jelenti egy pontjával és irányával, valamint az elforgatás szögét rögzítjük. Ez három meg két és még egy adat megadását jelenti, ez összesen hat adat, ugyan annyi, mint az előző esetben. Ezt a lehetőséget ritkán használjuk. A két változatot, - síkban - a 1-1a és b ábrán mutatjuk be.

1.2. A forgatási mátrix tulajdonságai

A forgatási mátrixot általánosan az 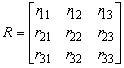formában írjuk fel.

1.

és

1.2.-1

a forgatási mátrix determinánsa 1-gyel egyenlő. Ezt nevezzük valódi forgatásnak. Ekkor a forgatás ugyanolyan sodrású koordináta rendszerek között történik. Ha a determináns értéke –1 akkor nem-valódi, vagy tükrözéses forgatásról beszélünk, ez a pontokat ellentétes sodrású koordináta rendszerbe viszi át. A forgató mátrixból kivonva az egységmátrixot 0 determinánsú mátrixot kapunk.

2.

1.2.-2

a forgatási mátrix inverze megegyezik transzponáltjával

3.

A sorok és oszlopok ortogonalitási feltételei

A sorok vektorának hossza 1-el egyenlő	Az oszlopok vektorának hossza 1-el egyenlő
A két sor szorzata 0-val egyenlő	A két oszlop szorzata 0-val egyenlő

a fentieket a következő rövidebb formában is írhatjuk

1.2.-3

Az előzőek alapján a 9 elem között 6 (kényszer) feltétel áll fenn, ezért csak 9-6=3 elem független.

4.

A forgatási mátrix egyes elemei a koordináta tengelyek irány-koszinuszai

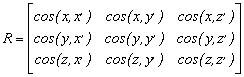
1.2.-4

5.

Bármely elem egyenlő a hozzá tartozó aldetermináns értékével

1.2.-5

6.

Az átlón kívüli szimmetrikusan elhelyezkedő elemek összegének és különbségének szorzata egyenlő

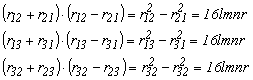
1.2.-6

A bizonyítást az 5.2.-3 képlete alapján láthatjuk.

7.

Bármely elem sorában lévő két másik elem négyzetének összege egyenlő az oszlopában lévő két másik elem négyzetének összegével. Ez az összeg egyenlő az elem négyzetének 1-től való különbségével.

1.2.-7

Ez következik az 1.2.-3 egyenletekből, a sorokra és oszlopokra felírt négyzetösszegek értékéből. De következik a tengely körüli forgatások egyenleteiből is, ha megnézzük a három tengely körüli forgatás első oszlopát és harmadik sorát, vagy a két tengely körüli forgatás első sorát és első oszlopát. Ha a tengely körüli forgatások sorrendjét megváltoztatjuk, akkor ezek a sorok és oszlopok mindig más-más helyre kerülnek. A négyzetösszeg átlón kívüli elem esetében a három tengely körüli forgatás középső szögforgatás koszinuszának négyzetével egyenlő, átlóban szereplő elem esetében a két tengely körüli forgatás középső szögforgatás szinuszának négyzetével egyenlő.

1.3. Jelölések

A dolgozatban lehetőség szerint egységes jelölést fogunk használni.

A forgató-mátrix elemeit, mint ahogy már megtettük,

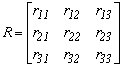
betükkel és indexekkel fogjuk jelölni.

Az Euler féle szimmetrikus paraméterek jelölésére az l, m, n, r betüket használjuk.

A ferdén szimmetrikus mátrixból felírt forgató-mátrix paramétereit e, f, g betükkel írjuk. Itt előforduló segédmennyiséget h-val jelöljük.

A Rodriques mátrix paramétereinek jelölését az a, b, c, és a segédmennyiség jelölését d betüvel végezzük.

A térbeli tengely körüli forgatás tengelyét c₁, c₂, c₃, irány koszinuszokkal jelezzük, az elfordulási szög jele: j lesz.

A tengely körüli forgatások leírásánál a három tengely körüli forgatásnál az elfordulási szögek jele a, b, g görög betükkel jelöljük az x, y, z tengelyek körüli forgatásokat.

A két tengely körüli forgatásnál a tengelyek körüli forgatásokat x₁, h, x₂ görög betűkkel jelöljük, a koordináta tengelyeknek megfelelően.

A hat Euler féle szögparamétereket görög betűkkel jelöljük.

1.4. A forgatási mátrixok összefoglalása

1.4.1. Euler négy szimmetrikus paramétere

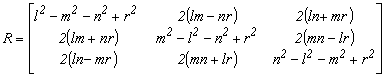
1.4.2. Ferdén szimmetrikus paraméterek

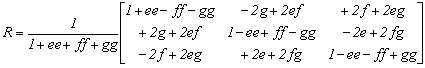
1.4.3. Rodriques paraméterek

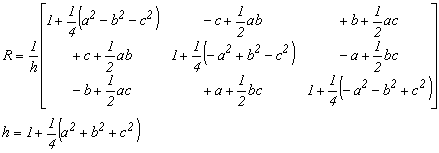
1.4.4. Térbeli tengely körüli forgatás

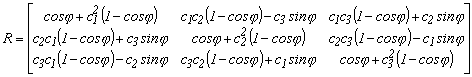
1.4.5. Átlón kívüli elemek különbsége

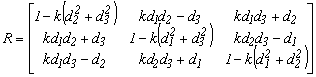
1.4.6. Euler forgatás három tengely körül

1.4.7. Euler forgatás két tengely körül

1.4.8. Euler hat szög-paramétere

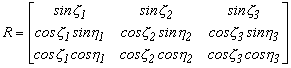
2. A forgatási mátrix paraméterei

A forgatási mátrix három független paraméter függvényeként állítható elő. Ezek felvételére többféle lehetőség van. Ebben a fejezetben ezek ismertetését tesszük meg.

2.1. Térbeli forgástengely körüli forgatás

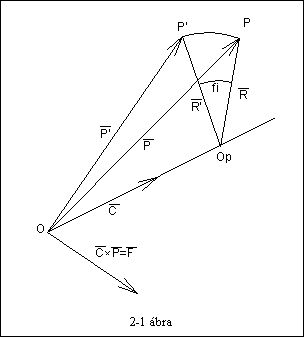Vegyünk fel egy pontot, melyen keresztül megy a forgástengely. Ez a pont lesz a koordináta rendszer kezdőpontja. A forgástengely irányát a C vektorral adjuk meg, a három iránykoszinusszal, ahol . Az elfordulás értéke j. A négy paraméter közül a három iránykoszinusz között fennáll az előbbi feltétel, így összességében csak három független paraméter van. Egy tetszőleges P pont koordinátái legyenek x, y és z értékűek. Ezt a P pontot forgassuk el j szöggel a felvett forgástengely körül (2-1 ábra).

Forgatás közben a P pont egy köríven mozdul el, melynek középpontja a forgástengelyre esik. Ez a pontot O_P–vel jelöljük. Először számítsuk ki a kezdőpontból a O_P–be mutató T vektort. A kezdőponttól mért távolságot a P és C vektorok skaláris szorzata adja, ezt a C vektorral való szorzással kapjuk meg a kezdőpontról az O_P pontba mutató vektort.

2.1.-1

A következőkben határozzuk meg az O_P pontból a P pontba mutató R vektort. A vektor szorzat a C és P vektorokra merőleges vektort ad eredményül, ennek nagysága megegyezik a O_P P távolsággal, de iránya arra merőleges. Ezt ismét megszorozva C vektorral, az eredő vektor hossza nem változik, de irányra már megfelelő lesz.

2.1.-2

A második egyenlőségben az R vektort, mint a pont P vektorának és ennek forgástengelyre eső vetületének különbségét képeztük.

Ezt az R vektort forgassuk el j szöggel a c tengely körül.

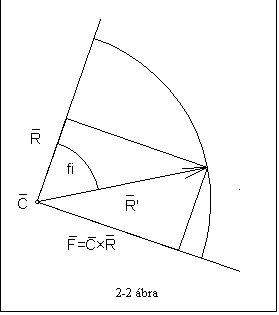Az elforgatott R¢ vektort a 2.-2 ábra szerint írjuk fel. Az ábrán a C tengelyt egy pontban látjuk, az R vektorra merőleges vektort a vektor szorzat adja. Az R vektor és a vektor egy derékszögű koordináta rendszert alkot. Ebben a rendszerben az elforgatott R¢ vektort az

2.1.-3

képlettel fejezhetjük ki. Az elforgatott P¢ pont helyét a

2.1.-4

vektor összeg adja. Fejtsük ki az egyes szorzatokat. A T vektor a következő lesz.

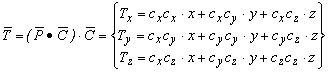
2.1.-5

Ez után írjuk fel előbb C´P vektor szorzatot

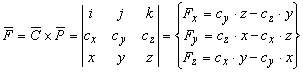
A következő lépésben számítsuk az R vektort

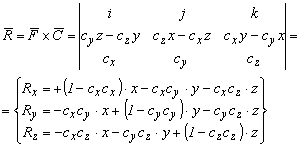
2.1.-6

És végül határozzuk meg a C´R vektor szorzatot.

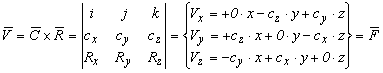
2.1.-7

Az előző képleteket írjuk be 2.1.-5 kifejezésbe

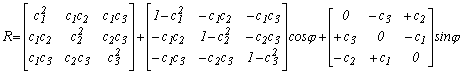
2.1.-8

A fentiekből láthatjuk, hogy a forgató mátrix egy elfordulási szögtől független és két elfordulási szögtől függő tagból tevődik össze. Ezek közül az első szimmetrikus, a második pedig aszimmetrikus mátrix.

Gyakrabban írjuk fel az előzőt a következő alakban.

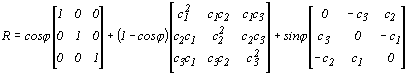
2.1.-9

A felírt képlet első két tagja a forgató mátrix szimmetrikus összetevőit mutatják, a szimmetriától való eltérést az utolsó tag hozza létre. A második tag mátrixát a forgástengelyirány-koszinuszainak szorzata adja, a szorzat formájában. A szorzatokat kifejtve az alábbi alakot kapjuk

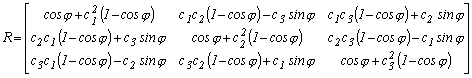
2.1.-10

A forgató mátrix elemeiből könnyen kifejezhetők a forgás-tengely irány-koszinuszai

Korn- Korn; Matematikai kézikönyv műszakiaknak

2.2. Az átlón kívüli elemek különbsége, mint paraméter

Az előző forgatási mátrixból egyszerűen levezethetünk egy olyan forgatási mátrixot, melyben az átlón kívüli elemek különbségei szerepelnek paraméterként. Osszuk el és szorozzuk meg az előző 2.1.-11 forgató mátrix elemeit sin²a-val. Vezessük be a

2.2.-1

Ezek beírása után a forgató mátrix

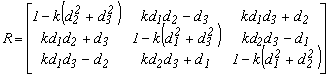
2.2.-2

A paraméterek között fenn áll a következő

2.2.-3

Az átlós elemek

2.2.-4

formában is felírhatók, de szebb az eredeti felírás, mert nem szerepel a j szög paraméterként.

2.3. Forgatási mátrix felírása ferdén szimmetrikus mátrixból

Forgatási mátrixot könnyen előállíthatunk ferdén szimmetrikus mátrixból.

A ferdén szimmetrikus mátrixot írjuk fel az alábbi módon

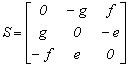és erre fenn áll, hogy

2.3.-1

és ebből számíthatjuk a forgatási mátrixot az

2.3.-2

összefüggésnek megfelelően. Végezzük el az előírt számításokat

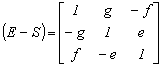
melynek determinánsa

és képezzük az adjungált mátrixot az inverz képzéséhez

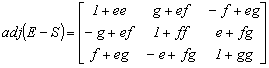
Ezután végezzük el az előírt szorzást

			1+ee	-g+ef	+f+eg
			+g+ef	1+ff	-e+fg
			-f+eg	+e+fg	1+gg
1	-g	+f	1+ee-gg -efg-ff+efg	-g+ef-g -ffg+ef+ffg	+f+eg+eg -fgg+f+fgg
+g	1	-e	+g+eeg+g +ef+ef-eeg	-gg+efg+1 +ff—ee-efg	+fg+egg-e +fg-e-egg
-f	+e	1	-f-eef+eg +eef+eg	+fg-eff+e +eff+e+fg	-ff-efg-ee +efg+1+gg

Ezzel a következő forgató mátrixot kapjuk

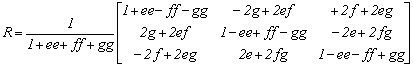
2.3.-3

Ez rokon a következőkben tárgyalandó Rodrigues mátrixszal és az Euler szimmetrikus paraméterekkel felírt mátrixával.

2.4. Forgatás Rodriques mátrixszal

Az előző mátrixhoz hasonlóan írhatjuk fel a Rodriques mátrixot is.

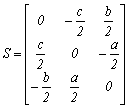
mátrix szorzata elvégzése után a következő forgató-mátrixot kapjuk.

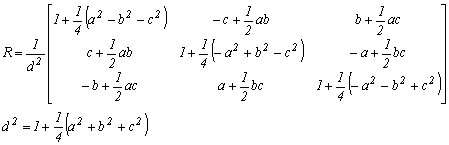
2. 4.-1

Ez természetesen szoros kapcsolatban van az előzőekben tárgyalt ferdén szimmetrikus paraméterekkel, és az Euler szimmetrikus paraméterekkel.

2.5. Euler szimmetrikus paraméterei

Euler négy szimmetrikus paraméterrel írja fel a forgató-mátrixot. Ez a ferdén szimmetrikus paraméterekből is származtatható. A négy paraméter között fennáll a következő feltétel

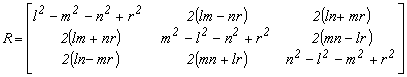
2. 5.-1

Ezt leggyakrabban a kvaternió algebra algebra segítségével vezetik le. A térbeli forgatás a következő kvaternió szorzás segítségével végezhető el.

ahol

az elforgatott pont vektora

az eredeti pont vektora

nem skalár egység kvaternió, a forgatás kvaterniója

a kvaternió inverze egység kvaternió esetén, konjugáltjával egyezik meg.

Végezzük el a kijelölt szorzásokat

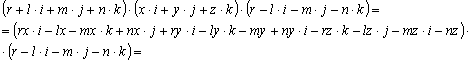
a konjugáltal számított szorzás

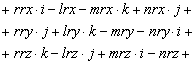
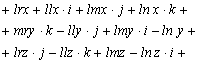
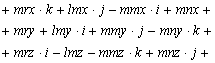
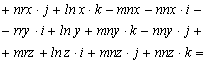
Amiből a forgató mátrix

	x	y	z
0
i
j
k

Az első sor elemei mind 0-val egyenlők.

A szorzásoknál figyelembe kell venni, hogy fenn állnak a vektorszámításnál ismert összefüggések

A felírt forgató-mátrix rokon a ferdén szimmetrikus mátrixból származtatottal. Ez jól látszik a felírt mátrix elemeinek hasonlóságából. A ferdén szimmetrikus és a Rodriqes paraméterek esetében van egy szorzótényező, itt ez egységnyi.

2.6. Koordináta tengely körüli forgatások

A forgatás leggyakrabban használt leírásában a forgatást tengely körüli forgatásokkal írjuk le.

Ez nagyon szemléletes, de felírásuk sok esetben nehézkes, ezért matematikailag nehezebben kezelhetők.

A forgató-mátrixot ebben az esetben az egyes tengelyek körüli forgatásokból írjuk fel. Az egyes forgatások mindig egymás után következnek és a következő forgatást a már elforgatott koordináta tengely körül végezzük. Ezért mondjuk, hogy a forgatások együtt mozgó koordináta rendszerre vonatkoznak.

Először írjuk fel az egyes tengelyek körüli forgatás mátrixait. A tengelyek körüli forgatásoknál, ahhoz a koordináta-tengelyhez tartozó koordináták, mely körül a forgatást végezzük változatlanok maradnak, és csak a másik két koordináta értékek változnak.

Először írjuk fel a síkbeli forgatás egyenleteit, a 2.6.-1. ábra alapján.

2-1. ábra. Koordináta tengelyek körüli forgatás

A síkbeli forgatásnál pozitív forgatásnál a koordináta rendszer x tengelyét forgatjuk az y tengely felé. Ez a bal sodrású és jobb sodrású rendszerekben is fenn áll. A felírt képletek mindkét sodrású rendszerben helyesek, csak más ábra tartozik hozzá.

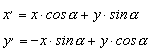
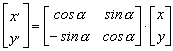
2.6.-1.

Ez alapján írjuk fel a térbeli tengelyek körüli forgató mátrixokat. mátrix a következő lesz.

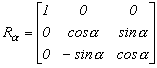
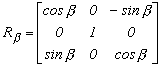
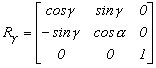
2.6.-2.

Az egyes tengelyek körüli forgatáskor a forgástengelyt követő koordináta tengely forog az őt követő tengely felé. A koordináták sorrendje az x-y-z, amely x-y-z sorrendben folytatódik.

Forgatás az x tengely körül a szöggel. Az y tengely fordul a z tengely felé.

Forgatás az y tengely körül b szöggel. A z tengely fordul a x tengely felé.

Forgatás az z tengely körül g szöggel. Az x tengely fordul az y tengely felé.

Térbeli forgatások két formában állíthatók elő tengely körüli forgatásokkal. A gyakoribb esetben mind a három tengely körül forgatunk, meghatározott sorrendben. A másik esetben két tengely körül forgatunk. Először a kiválasztott első tengely körül, majd egy másik tengely körül forgatunk, és végül ismét az első tengely körül végezzük a forgatást, egy eltérő szögértékkel. A tengely körüli forgatásoknál a forgató-mátrixot úgy kapjuk, hogy az egyes tengely körüli forgató mátrixokat megfelelő sorrendben összeszorozzuk.

Ezeket a forgatásokat Euler szögekkel végzett forgatásoknak nevezzük, mert részletes ismertetésük tőle származik.

2.7. Euler forgatás három tengely körül

A három tengely körüli forgatásnál a három tengely sorrendjét tetszőlegesen választhatjuk ki. Ez összességében hat lehetőséget jelent. (xyz, xzy, yxz, yzx, zxy, zyx)

Mi, válasszuk a természetesnek tűnő első lehetőséget.

1. forgatás az x tengely körül szöggel, 2. forgatás az y tengely körül szöggel, 3. forgatás a z tengely körül szöggel.

A forgató mátrixot ennek megfelelően a következő sorrendben állítjuk elő.

2.7.-1.

Ezzel a transzformációt az alábbi módon számíthatjuk.

Végezzük el a kijelölt szorzásokat

2.7.-2

2.8. Forgatás két tengely körül

Két tengely körüli forgatásnál a tengelyek sorrendjét szintén megválaszthatjuk. Ekkor is 6 különböző eset lehet. (xyx, xzx, yxy, yzy, zxz, zyz). Mi most is az első esetet választjuk, és ennek megfelelően írjuk fel a forgató mátrixot.

Először az X tengely körül szöggel, másodszor az Y tengely körül szöggel, és harmadszor az X tengely körül szöggel forgatunk.

2.8.-1

Az x tengely körüli forgatáskor az y tengelyt forgatjuk a z tengely felé.

Az y tengely körüli forgatáskor az z tengelyt forgatjuk az x tengely felé.

A z tengely körüli forgatáskor az x tengelyt forgatjuk az y tengely felé.

Ezért cserél helyet a sinh előjele az y tengely körüli forgatáskor.

2.9. Euler hat szög paramétere

Euler 1775-ben adott egy forgató mátrixot, melyben 6 szög paraméter szerepel. A forgatási mátrixot az alábbi módon írja fel

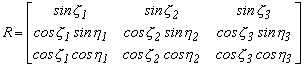
2.9.-1.

2.9.-2

és

2.9.-3

Ezek az összefüggések megadják a kapcsolatot a hat paraméter között.

A forgatás három független paramétereként két eset lehetséges. Független paraméterként választhatjuk az h₁ h₂ h₃ szögforgások értékét. Másik lehetőség a z₁ z₂ h₁ szögértékek megadása.

Az h₁ h₂ h₃ megadásakor először számítjuk a D értékét a 2.8.-2 második képletével, majd a z₁ z₂ z₃ szögeket a 2.8.-3 képletekkel határozhatjuk. Ezzel meghatároztuk a hat szög paramétert és felírhatjuk a forgató mátrixot.

A második esetben a harmadik z₃ szöget az első sor egységnyi hossza alapján a

képlettel számíthatjuk, majd képezhetjük a D értékét a 2.9.-2 első összefüggésével. Ezután az h₁ h₂ h₃ szögek különbségeit határozhatjuk meg a

képletekkel, a koszinusz visszakeresése után. Ezután számítsuk a

és

szögeket. Ellenőrzést többféleképpen végezhetünk, például Számíthatjuk az . h₁ szöget a másik két szögből, vagy meghatározhatjuk a D értékét a koszinusz összefüggésből. Legjobb ellenőrzés azonban, ha a kiszámított szögekből meghatározzuk a forgató mátrixot és ellenőrizzük annak ortogonalitását.

2.10. A három átlón kívüli elem, mint paraméter

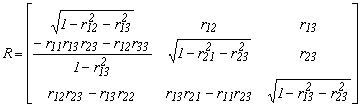
2.10.-1

fejezzük ki az -et aldeterminánsként, és ebbe írjuk be az ismeretlen elemhez tartozó aldeterminánst:

mivel és az így kapott egyenletből kifejezhetjük az értékét az alábbi formában: . Ezután számíthatjuk a többi hiányzó elemet is.

A meghatározás másik lehetősége, hogy az elemet számítjuk hasonló módon:

amibe az értékét írjuk be aldetermináns formájában. . Az így kapott egyenletből az kifejezést kapjuk.

2.11. Forgatás kis szögekkel, közelítő forgatás

A forgatási mátrix felírását gyakran kis szögekkel írjuk fel. Ezt a forgató mátrixot többféle képen származtathatjuk. Leggyakrabban a három tengely körüli forgatásból vezetjük le. A felírt 2.6.-2 összefüggéseket írjuk fel kis szögekkel. Kis szögek esetén az a, b és g szögek szinuszai függvényei ívmértékükkel egyenlő, a szögek koszinuszai 1-el lesznek egyenlők.

2.11.-1

Két kis szög szinuszának szorzatát 0-nak vesszük. Ezzel a forgató mátrix az alábbi lesz:

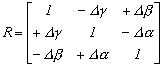
2.11.-2

Származtathatjuk az Euler paraméterekből is, kis forgatásnál az

l=Dl, m=Dm és n=Dn lesz, az r=1

2.11.-3

értékű lesz. A ferdén szimmetrikus paraméterek esetében az

e=De f=Df és g=Dg

2.11.-4

kis értékek lesznek. A térbeli tengely körüli forgatásnál a térbeli tengely körüli elforgatási szög lesz kis értékű,

j=Dj

2.11.-5

A forgástengely irány koszinuszai nem lesznek kis számértékek.

A forgató mátrixot ezek alapján a következő formában írhatjuk fel kis elfordulási szög esetén:

.

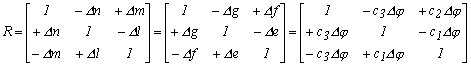2.11.-6

A felírt elemi forgatás mátrix mindhárom esetben egyezik a három tengely körüli forgatásból felírttal, csak az elemi forgatási paraméter értéke más magyarázatból származik.

Ez a mátrix egyezik a ferdén szimmetrikus paraméterek eredeti

R=E+S

2.11.-7

mátrixával.

A két tengely körüli forgatásból ezt a mátrixot nem lehet felírni.

Gyakorlati szempontból ennek az elemi forgatómátrixnak nagyon sok alkalmazása van. A forgatási mátrix kiegyenlítéssel való meghatározásánál.

3. A forgatási paraméterek kapcsolata

3.1. Az Euler-féle, a ferdén szimmetrikus és a Rodriques paraméterek kapcsolata

A Euler szimmetrikus paraméterek, a ferdén szimmetrikus paraméterek és a Rodriques paraméterek alapján felírt forgató-mátrixok sok hasonlóságot mutatnak. Ezek alapján vizsgáljuk meg a köztük fennálló kapcsolatot.

Az arányossági tényező az Euler paraméternél 1-el egyenlő. A Rodriques paramétereknél

A ferdén szimmetrikus paraméterek esetén ez

-vel egyenlő.

A forgatómátrix első sorának első elemét a következőképpen írhatjuk a Rodriques paraméterekkel

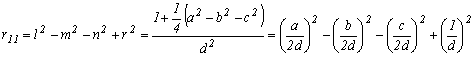
Ugyanez a ferdén szimmetrikus paraméterekkel felírva

Ebből már felírhatjuk a paraméterek kapcsolatát

ahol

3.1.-1

A Rodriques paraméterek kifejezve a másik két paraméter csoporttal

3.1.-2

és a ferdén szimmetrikus paraméterek a

3.1.-3

képletekkel írhatók fel.

A felírt összefüggések alapján láthatjuk, hogy a kapcsolat nagyon szoros, ez lehetővé teszi hogy a többi forgató-mátrixszal való kapcsolatokat együtt vizsgáljuk. Ezek közül is az Euler paraméterek fontossága igen jelentős, mert a forgató-mátrixban az arányossági tényező 1-el egyenlő.

3.2. Az Euler paraméterek kifejezése a forgástengely valamint a két tengely körüli forgatás kapcsolata

Az Euler paraméterek és a forgástengely valamint a két tengely körüli forgatás közötti kapcsolat a következő formában írható fel

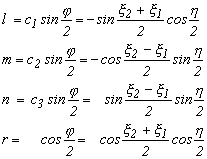
3.2.-1

Ez alapján könnyen kifejezhetjük a Euler paraméterekkel a forgás tengely irány-koszinuszait és az elfordulási szöget

3.2.-2

3.3. A Euler tengely körüli forgatás szögértékeinek meghatározása Euler paraméterekkel

A 4. fejezetben leírjuk a forgásszögek számítását a forgatási mátrix elemeiből.

A 4.4.-5 képletekbe írjuk be az elemek Euler paramétereit, rendezés után a következőt kapjuk:

és

3.3.-1

Hasonlóan ezt megtehetjük a 4.5.-5 összefüggés esetén is:

és

3.3.-2

Az h szög meghatározását a 4.5.-1 és a 4.5.-2 képletek segítségével végezhetjük, ezekbe a forgató-mátrix elemei helyére írjuk be az Euler paramétereket:

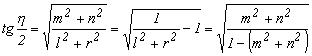
3.3.-3

4. A paraméterek meghatározása a forgatási mátrixból

4.1. A forgás-tengely meghatározása

Írjuk fel az átlón kívüli elemek különbségeit

Számítsuk ki a főátló nyomát

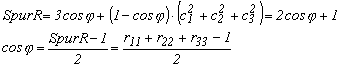
Az elfordulási szög szinusza az átlón kívüli elemek különbségéből

ebből a forgástengely irány-koszinuszai és az elfordulási szög

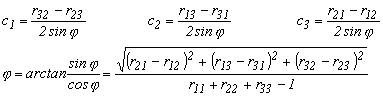
4.1.-1

a szögnegyedet a szinusz és a koszinusz előjele határozza meg. Ha a számlálót, a gyökvonás miatt, mindig pozitív értékűnek vesszük akkor az elfordulási szög midig kisebb lesz, mint 180°. Ennek megfelelően 180°-nál nagyobb elfordulás esetén visszaszámolva a forgató-mátrixból a forgástengely ellentétes irányú lesz, úgy, hogy az elfordulási szög 180°-nál kisebb legyen.

4.2. Az Euler paraméterek meghatározása

Képezzük a főátló nyomát

és ebből az r paraméter

4.2.-1

Az átlón kívüli elemek különbségei

és így

4.2.-2

képletekkel számíthatjuk a hiányzó három paramétert.

Az r kifejezésében gyökvonás szerepel, ezért az r előjele mindig pozitív lesz, ennek megfelelően alakulnak a további paraméterek. Az l, m, n, r forgatás és a -l, -m, -n, -r ugyanazt a forgatást állítja elő. Így pozitív előjelű r esetén is van egyértelműen meghatározható paraméter négyes.

A forgató-mátrix elemei és az Euler paraméterek között felírható néhány jellegzetes összefüggés.

Az átlón kívüli elemek összege	Az átlón kívüli elemek különbsége	Euler paraméterek négyzete az átlós elemekből

4.2.-3

Ezek a képletek lehetővé teszik a paraméterek kifejezését. Ez különösen a ferdén szimmetrikus paraméterek meghatározására érvényes.

Az alább felírt összefüggésekben az Euler paraméterek hányadosának értékét a forgató mátrix elemeivel fejezzük ki. A második és harmadik egyenlőségjel után az átlón kívüli elemek összegének és különbségének hányadosaival határoztuk meg. A negyedik egyenlőség után az átlón kívüli elemekből számítottuk. Végül az ötödik képletek az átló elemeiből és az aszimmetrikus elemek különbségéből való számítási lehetőséget mutatja.

4.2.-4

Ezek az összefüggések már inkább a következő fejezethez tartoznak.

4.3. Ferdén szimmetrikus paraméterek meghatározása

A mátrix felírása hasonló az Euler paraméterekkel felírt mátrixhoz. Ezért itt is hasonló módon végezzük a számítást. Először a mátrix nyomát képezzük

amiből a forgató-mátrix szorzótényezőjének reciproka

Az átlón kívüli elemek különbségei

és így

4.3.-1

Ezenkívül nézzük meg az előző fejezet 4.2.-4 összefüggéseit.

4.4. Három tengely körüli forgás-szögek meghatározása

Három tengely körüli forgatás forgás szögeit a forgatási mátrix első oszlopa és harmadik sora elemeiből számíthatjuk.

A harmadik sor második és harmadik eleméből

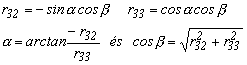
4.4.-1

A fenti összefüggéssel számíthatjuk az a szöget. Az a szög-negyede az együtthatók előjeléből határozható meg, és hasonlóan Számíthatjuk a g szöget is.

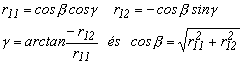
4.4.-2

A b szög meghatározásához az eddigiekből már ismerjük koszinuszának értékét, a gyökvonás miatt mindig pozitív előjellel.

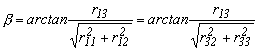
4.4.-3

formában határozható meg.

A b szög-negyede az együtthatók előjeléből határozható meg. Értéke azonban midig 270°-360°=0° és 90° fok közzé esik, mert a koszinuszát pozitívnak tételeztük fel. Az a és b szögeket is ezzel a feltétellel számítottuk. Ha ezekkel a szögértékekkel ismét számítjuk a forgató mátrixot ugyanazt kapjuk meg, mert az R(a, b,g)=R(a+180°, 180°-b, g+180°) forgatással.

A forgatás szögértékeit számíthatjuk más módon is. Írjuk fel az r₁₂ és az r₂₃ elemek összegét és különbségét, valamint ugyanezt az r₁₃ és az r₂₂ elemekre is.

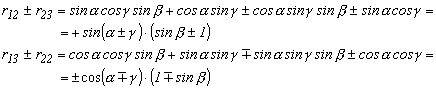
Ebből felírhatjuk a szögek összegének szinuszát és koszinuszát felhasználva, hogy egyenlő:

4.4.-4

Ezekből felírhatjuk a szögek felének tangensét a összefüggések felhasználásával:

4.4.-5

4.5. Két tengely körüli forgás-szögek meghatározása

A két tengely körüli forgatás paramétereit az előzőhöz hasonlóan határozzuk meg. Az első sor második és harmadik eleméből a x₁ kifejezhető:

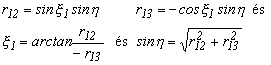
4.5.-1

a x₁ szög-negyede az együtthatók előjeléből határozható meg, azzal a feltételezéssel, hogy a sinh előjele pozitív. Hasonlóan a x₂ is meghatározható a forgató mátrix első oszlopának elemeiből. Ekkor is ugyanazzal a feltételezéssel élünk mint az előbb.

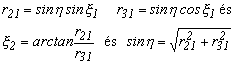
4.5.-2

Az h szög számítását megint csak tangenséből számítjuk

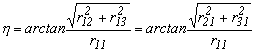
4.5.-3

A forgásszögek nem mindig egyeznek az eredeti szögekkel. Ugyanazt a forgatómátrixot más forgásszögekkel is előállíthatjuk. az R(x₁, h, x₂)=R(x₁+90°, h, x₂-90°) ugyanazt a forgató-mátrixot állítja elő.

Az előzőhöz hasonlóan ennél a forgatásnál is meghatározhatjuk a forgásszögek összegét és különbségét. Írjuk fel az r₂₂ és az r₃₃ elemek összegét és különbségét, valamint írjuk fel ugyanezt az r₂₃ és az r₃₂ elemekre is.

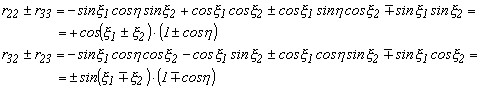
Ebből felírhatjuk a szögek összegének szinuszát és koszinuszát felhasználva, hogy egyenlő:

4.5.-4

Ezekből felírhatjuk a szögek felének tangensét a összefüggés felhasználásával:

4.5.-5

4.6. Paraméterek számítása a forgatási mátrixból

A következőkben számpéldán keresztül mutatjuk be az elmondottakat. Legyen a forgató mátrix az alábbi:

+0.262 002 6	+0.964573 8	+0.030 855 1
-0.719 846 3	+0.174 033 5	+0.671 962 5
+0.642 787 6	-0.198 266 9	+0.739 942 1

Határozzuk meg a forgástengely irány koszinuszait és az elfordulási szöget, az 4.1.-1 képletekkel. (2sinj = +0.992 242 9, 2cosj = +0.175 978 2)

c1=- 0.436 808 9	c2=- 0.307 157 6	c3=- 0.845 489 3
j=+84° 57¢ 07.4²

Számítsuk ki az Euler paramétereket az 4.2.-1 és az 4.2.-2 összefüggésekkel:

l=- 0.294 969 1	m=- 0.207 417 9	n=- 0.570 943 5
r=+ 0.737 559 9

Ferdén szimmetrikus paraméterek számítása az 4.2.-4 és az 4.3.-1 kifejezésekkel:

e=- 0.399 925 7

f=- 0.281 221 8

g=- 0.774 097 9

A h²=1.838 253 7 értékűre adódott.

A három tengely körüli forgatás szögértékeket az 4.4.-1, 4.4.-2 és a 4.4.-3 összefüggésekkel határozhatjuk meg. (cosb=0.766 044 4)

a=15° 00¢ 00.0²

b=40° 00¢ 00.0²

g=70° 00¢ 00.0²

Ez egyezik az eredeti felvétellel, mert az eredeti forgató mátrixot ebből számítottuk.

A két tengely körüli forgatás elfordulási szögeit az 4.5.-1, 4.5.-2 és az 4.5.-3 kifejezésekkel számíthatjuk: (sinh=0.965 067 2)

x1=91° 49¢ 55.8²

h= 74° 48¢ 39.9²

x2=-48° 14¢ 12.1²

A szögek összege és különbsége: a+b=43° 35¢ 43.7², a-b=140° 04¢ 07,9²

A számításokat Matlab programmal végeztük, a paraméterek számítása után felírtuk a forgató-mátrixot is és az egyezett az eredeti forgató mátrixszal.

Kapcsolatos Matlab program: kapcs3.m.

Legyen a forgató mátrix a későbbiekben számított kiegyenlített forgató mátrix:

+0.29615521768158	+0.94146156021345	+0.16106587993871
-0.81360287185407	+0.16032108767828	+0.55888059167989
+0.50034233675633	-0.29655906576280	+0.81345575575019

A legnagyobb eltérés a forgató mátrix ortogonalitási feltételeiben: 3.4416e-015

Euler forgatás három tengely körül:

a=20.03018299052931°

b=30.02265140317529°

g=69.99825948812584°

Euler szimmetrikus paraméterei

l=-0.28389186949132	m=-0.11259453166841	n=-0.58244730456719
r=+0.75331468542536

Ferdén szimmetrikus paraméterek

e= -0.37685694303307

f= -0.14946546754871

g= -0.77317927797771

Paraméterek hossza: 1.76216727739592

Rodriques paraméterek

a= -0.75371388606614

b= -0.29893093509742

c= -1.54635855595542

Paraméterek hossza: 1.76216727739592

Euler forgatás két tengely körül

x1=+99.70821353890342°

h=+72.77317779106365°

x2=-58.40968147333469°

Térbeli tengely körüli forgatás

c1 = -0.43166950710350

c2= -0.17120471281880

c3 = -0.88563558134576

Elfordulási szög: j=+82.24334439453386°

Kapcsolatos Matlab program: par.m.

5. A forgató mátrix meghatározása kiegyenlítéssel

5.1. A kiegyenlítés javítási egyenletének felírása

A transzformációs egyenletet az

formában szoktuk felírni, ahol

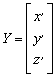
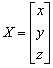
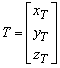
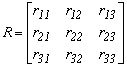
5.1.-1

Y az áttranszformált pont koordinátái, X az átszámítandó pont koordinátái, T az eltolási paraméterek, R a forgatási mátrix.

Ha több pontot kell átszámítani, akkor kedvezőbb a transzformációs egyenletet a következő formában felírni:

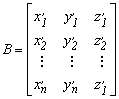
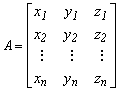
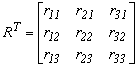
5.1.-2

Ezekben a mátrixokban az átszámítandó koordinátákat A, az átszámítottakat a B mátrixban foglaltuk össze. A javítási egyenleteket úgy írjuk fel, hogy csak az átszámított pontokat tekintjük hibátlannak, így a javítási egyenlet a következő lesz:

ahol

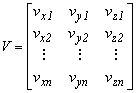
5.1.-3

Ebből a javítási egyenletet legtöbbször az alábbi formában írjuk fel:

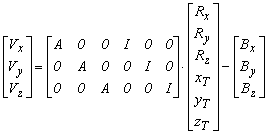
5.1.-4

Ebben a javítási egyenletben a második rendszer koordinátáit B_x , B_y és B_z vektorokra bontottuk, hasonlóan javításokat is V_x , V_y és V_z tengely irányú javításokra és a forgató mátrixot is R_x , R_y és R_z oszlopokra bontottuk. Az így felírt javítási egyenleteket még ki kell egészíteni a paraméterek között fennálló kényszerfeltételekkel,

Az ebből felírható normál egyenletrendszer:

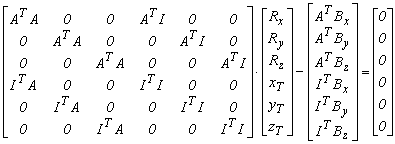
5.1.-5

Ha az első és a második koordinátákat is súlyponti koordinátákra számítjuk át, akkor az A^TI és az I^TB szorzatok 0–val lesznek egyenlők:

5.1.-6

Ezzel az egyenletrendszer egy kilenc ismeretlenes egyenletté és három egy ismeretlenes egyenletté esik szét. Ez azzal az előnnyel is jár, hogy a forgató mátrix elemeinek meghatározásánál nem szükséges paraméterként az eltolás három összetevőjét is szerepeltetni. Az eltolás mértéke a két rendszer súlypontjainak különbsége.

5.1.-7

Azonban, ha az átszámított pontok pontosságát is számítani akarjuk, akkor figyelembe kell venni az eltolási paraméterek súlykoefficienseit is.

A felírt javítási egyenletekhez még hozzá tartozik a forgató mátrix elemei között fennálló kényszerek egyenletei is.

5.2. Kiegyenlítés az ortogonalitási kényszerek felírásával

5.2.1. Merőlegességi kényszerek felírásával

Az 5.1.4 javítási egyenletekhez vegyük hozzá az 1.2.-3 feltételeket, kényszerként.

A kényszerfeltételekben csak olyan elemek szerepelnek, melyek meghatározandó paraméterek. Ezek értékét nem ismerjük, ezért a kényszer feltételi egyenleteket csak közelítően tudjuk felírni, valamilyen előzetes értékek alapján. Előzetes értékként számíthatjuk az affin transzformációs mátrixot, és ezeket használjuk fel első közelítő értéknek. A megoldás így iterációs megoldássá válik. A második és minden további iteráció kezdetén előzetes értékeket az előző iterációban a kényszerfeltételbe beírt és a kiegyenlítés után a meghatározott együtthatók számtani középértékeként vesszük fel és ez lesz a következő iterációban a kényszerfeltétel együtthatója.

Az első oszlopban szereplő három kényszer felírása így egyértelmű. A második oszlopban lévő skaláris szorzatokat azonban többféleképpen is felírhatjuk, aszerint, hogy a szorzat melyik tényezőjét tekintjük ismeretlennek, és melyiket helyettesítjük közelítő értékkel. A következőkben a forgató mátrix egyes sorait jelöljük r_x , r_y és r_z vektorokkal.

A különböző felírási lehetőségek a következők:

5.2.-1

Itt minden szorzatnál az első tényezőt tekintjük a kényszer feltétel együtthatójának a második tényező pedig a paraméter. A felírható kényszerek számát tovább növeli, hogy a kényszereket a forgató mátrix oszlopaira is felírhatjuk, mint ahogy azt az 1.2.-3 egyenletekben is láttuk.

A különböző felírások nem azonos kiegyenlítési eredményeket adnak. Más lesz a forgató mátrix, és eltérnek a javítások is.

5.2.2. Kilenc kényszer felírásával

Az előzőekben láttuk, hogy a kényszereket különböző módon felírva eltérő eredményeket kapunk. A kényszerek felírását valamilyen módon egyértelművé kell tenni. Ennek több lehetősége van. Az egyik lehetőség az, hogy kétszer írjuk fel a skaláris szorzat feltételeit, így a három feltétel helyett hat feltételt írunk fel, melyek nem függetlenek, de elérjük, hogy minden együttható és paraméter azonosan szerepel a feltételekben.

5.2.-3

Ezzel a normál egyenletrendszer mérete megnövekszik. Már korábban is a 9 paraméter meghatározásához 6 kényszert kell hozzáírni, ezzel a normál egyenletrendszer 15 ismeretlenes volt, ez most további 3 ismeretlennel növekszik, és 18 ismeretlenessé válik.

A számítási tapasztalatok alapján a kényszerek ilyen felírása esetén a javítások négyzetösszege nem lett a legkisebb, egyes esetekben a más módon felírt kényszerekkel job megoldást kaptunk.

5.2.3. Kettős merőlegességi kényszer felírásával

A három skaláris szorzatot egyértelműen úgy írhatjuk fel, hogy mindegyiket kétszer írjuk be a kényszerfeltételi egyenletbe, az alábbi példának megfelelően,

5.2.-2

Mindhárom feltételt ilyen kettős feltétel formájában írunk fel. Ezzel elérjük, hogy mindegyik paraméter és együttható ugyanolyan felírással szerepel. A normál egyenletrendszer mérete sem növekszik, és az eredeti felírásnak megfelelően továbbra is 9+6=15 ismeretlenes lesz.

A kiválasztott mintapéldánál az iterációk is jól alakultak, gyorsan eredményre vezetettek.

A iterációk esetén a normál egyenletrendszer együttható mátrixa az iterációk során nem változik, csak a kényszerfeltételek együtthatói változnak. Az iterációk során áll be a transzformációs mátrix merőlegességi feltételeinek teljesülése is.

(A kapcsolatos Matlab program: W**.M)

5.3. Kiegyenlítés a forgató mátrix inverzének kényszere alapján

A forgatómátrix tulajdonságainál láttuk, hogy a forgatómátrix inverze egyenlő a transzponáltjával az 1.2.-2 képlet szerint. A kiegyenlítés javítási egyenletét írjuk fel az 5.1.-3 egyenletnek megfelelően, ezekből hagyjuk el az eltolási paramétereket, tehát térjünk át a súlyponti koordináta rendszerre

5.3.-1

Itt a javítások is egy mátrixban szerepelnek, egy sorban egy koordinátának x, y és z irányú javításai. Ehhez vegyük hozzá az 1.2.-3 egyenletet, mint kényszerfeltételt.

5.3.-2

ahol E egy 3´3-as egységmátrix.

Ebből a normál egyenletrendszer az alábbi

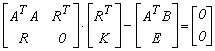
5.3.-3

Itt a K egy 3´3 korreláta mátrix, a három 0 mátrix is 3´3 méretű 0 elemű mátrixok. A normál egyenletrendszer mérete is 6´6–os. Ez a megoldás is iterációs, mert a kényszer feltételben a meghatározandó R forgató mátrix szerepel.

A kiegyenlítés kezdetén az előzetes forgató mátrixot egy előzetes kiegyenlítéssel meghatározott affin transzformációs mátrixként vettük fel. Minden további iterációnál a következő előzetes forgató mátrixot a kiegyenlítés sorrá meghatározott forgató mátrix és az előző előzetesen felvett mátrix középértékeként számítjuk.

A javításokat is egy n´3 méretű mátrixban kapjuk meg. A javítások négyzetösszegét egy 3´3-as mátrixként kapjuk meg, melynek nyoma lesz a javítások négyzet összege.

A számpéldák során a megoldás igen gyors iterációt eredményezett. A kapott forgató mátrix, a javítások és azok négyzetösszege is azonos volt a 9 ortogonális feltétel felírásával kapott eredményekkel.

(A kapcsolatos Matlab program: R**.M)

5.4. Kiegyenlítés kis szögekkel meghatározott forgatással

A geodéziában elvégzett forgatások esetén leggyakrabban ezt a kiegyenlítést alkalmazzák. A megoldásnál, ha a pontok között jelentős mértékű elfordulás van, akkor egy előzetes forgatással elvégezzük a pontok közelítő áttranszformálását. Ezt egyszerűen úgy oldhatjuk meg, hogy előzetesen egy affin transzformációs paramétereket határozunk meg kiegyenlítéssel és ezt forgatómátrixnak tekintve a 4.4 fejezetben leírtaknak megfelelően számítjuk a három elfordulási szög értékét a 4.4.-1 –4.4.3 képletekkel. Ebből számíthatjuk a közelítő forgatás mátrixát a 2.6.-2 összefüggésekkel. Ezután közelítőleg átszámíthatjuk a pontokat a második rendszerbe, és így a két rendszer között már csak kis elforgatás szükséges, a meghatározandó forgató mátrix most a 2.9.-2 alapján a következő alakú

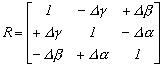
A javítási egyenleteket a forgató mátrix 2.9.-2-ben felírt alakjával végezzük

Így a korábban súlyponti koordinátákra felírt

egyenletben az R^T mátrix már lineáris. Így a javítási egyenletrendszer a következő

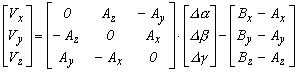
6.4.-1

itt az A mátrixban az első rendszerbeli közelítően áttranszformált koordináták szerepelnek. A felírt javítási egyenletrendszerben 3 paraméter szerepel és a pontok számának 3 szoros egyenlet van.

A kiegyenlítés után meghatározott paraméterek csak közelítő értéknek tekinthetők, mert ha nem kis értékek, akkor a forgató mátrix csak közelítő. E miatt a kiegyenlítés csak közelítő és a kiegyenlítés iterációs eljárássá válik. A következő iterációnál a kiegyenlítést meg kell ismételni úgy, hogy az eredeti A első rendszerbeli koordinátákat ismét átszámítjuk a

6.4.-2

összefüggéseknek megfelelően, és ezekkel megismételjük az első rendszerbeli koordináták újraszámítását, és a kiegyenlítést újból elvégezzük.

A számítási tapasztalatokból láttuk, hogy az iteráció több esetben igen lassan és egyes estekben rosszul következett be. Az iterációnál az egyik lépés után a javítások négyzetösszege nőni kezdett és az eredmény teljesen eltorzult. Az iteráción néhány esetben segíteni lehetett azzal, hogy az elforgatás szögét egy arányszámmal csökkentettük.

(A kapcsolatos Matlab program: B**.M)

5.5. A ferdén szimmetrikus paraméterek kis változásainak számítása kiegyenlítéssel

A 2.9. fejezetben felírtunk még kis elforgatására vonatkozó képletet 2.9.-6 számmal:

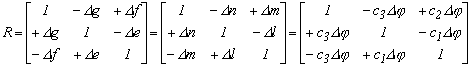
A felírt kis elforgatású forgató mátrixok ugyan olyan alakúak, mint az előző fejezetben tárgyalt három tengely körüli kis Euler szögekkel végzett forgatás. A megoldás ezekben az esetekben is nagyon hasonló. A kiegyenlítés ugyanúgy történik, csak a meghatározott paraméterek értelmezése más.

Az első felírás szerinti megoldásnál először az ismert affin transzformációs mátrixot határozzuk meg kiegyenlítéssel. Ezt egy közelítő forgató mátrixnak tekintjük és a 4.2.-4 vagy a 4.3.-1 összefüggésekkel kiszámítjuk az e f g paramétereket. Ebből számítjuk a forgató mátrixot a 2.2.-3-nak megfelelően. Ezzel átszámítjuk az első rendszerbeli pontokat a második rendszerbe az 5.1.-3 első képlete szerint. A kiegyenlítést ezek között végezzük el.

A javítási egyenleteket most is a 6.4.-1 formában írjuk fel. A meghatározott De Df Dg paramétereket Adjuk hozzá a paraméterek közelítő értékéhez és meg kapjuk a következő értékeket, melyekkel megismételjük a kiegyenlítést, ezt addig folytatjuk, amíg a változások 0 értékűek nem lesznek.

(A kapcsolatos Matlab program: C**.M)

5.6. Az Euler paraméterek kis változásainak meghatározása

A második megoldásnál hasonló módon jártunk el. A paramétereket itt is mindig az előzőekben leírt módon határoztuk meg. A negyedik paramétert minden esetben az l, m és n paraméterek számítása után a feltételnek megfelelően számítottuk a r értékét. A forgatómátrix minden közelítéskor pontos volt, tehát kielégítette a forgató mátrix feltételeit. A példák során tapasztaltunk olyan esetet is, melynél a iteráció folyamatosan lefutott, de az iterációk között volt olyan, melynél a javítások négyzetösszege kisebb volt mint, a végeredményé. A megoldás több esetben elszállt, azaz az iterációk egy darabig végzet szép csökkenés után, elkezdett emelkedni és a végén durva eltéréssel állt meg.

Az iterációk javíthatók azzal, hogy a kiszámított paraméter változás csak egy részét adtuk hozzá, ezzel lassítva az iterációt. Ha csökkent a javítások négyzetösszege akkor a csökkentés értéke 1-2 között változott, ha növekedés történt akkor ennél nagyobb 2-10 szeres osztót alkalmaztunk.

A különböző példák kiegyenlítése esetén több esetben gyenge iterációt tapasztaltunk.

(Kapcsolatos Matlab program:, D**.M )

5.7. Térbeli tengely körüli elemi elfordulás meghatározása

A harmadik képlet szerinti megoldásnál kicsit másképpen jártunk el. A meghatározása után számítottuk a forgástengely iránykoszinuszait és a kis elfordulási szöget. Ezekből meghatároztuk a forgatási mátrixot, amivel megszoroztuk ez előző forgatási mátrixot, így kaptuk a következő forgatás mátrixát.

5.5.-1

Ezt azért tesszük mert itt a paramétereket nem lehet összeadással számítani. Ilyen megoldást az előző kiegyenlítések esetén is alkalmazhatunk.

A megoldás most is iteráció, a tapasztalatok szerint ennél kaptunk a legjobb közeledést. Minden mintapéldát közvetlenül meg lehetett oldani, ami más megoldásoknál csak nehezen sikerült.

(Kapcsolatos Matlab program:, E**.M )

5.8. Az iterációs megoldások tapasztalatai

Az előzőekben bemutatott kiegyenlítések mind iterációs eljárások. Lényegében két csoportba sorolhatók, az első esetben a forgató mátrixot kényszerek segítségével állítottuk elő, a második esetben a forgató mátrixot közelítő paraméterek segítségével határoztuk meg.

A lényeges különbség a kettő között az, hogy az első esetben a forgatómátrixnak kell előállni az iterációk során, míg a második esetben a közelítő paraméterek alapján felírt helyes forgató mátrixnak kell befordulni a jó helyzetbe. Mindkét esetben a javítások négyzetösszegét minimalizáljuk, úgy, hogy más feltételnek is teljesülni kell.

Nézzük részletesebben a ortogonalitási feltételek felírását. Ekkor a javítások négyzetösszegének minimalizálása mellett a forgató mátrix hat feltételének is teljesülni kell. A kiegyenlítés során az előzetes közelítő forgató mátrixot minden ciklus után módosítjuk. Nem elegendő figyelni a négyzetösszeg minimumát és ennek változását figyelni, hanem a kényszer feltételek teljesülését is figyeljük. Ezenkívül a forgató mátrix változásait is figyelni kell. A ciklusuk lefutásakor átmenetileg nőhet a javítások négyzetösszege, ez majd később csökkenni fog. A különböző példák megoldásakor általában elfogadható lefutásokat tapasztaltunk. A ciklusok lefutásakor ezek máshogy és máshogy teljesülnek. Csak akkor fogadhatjuk el a számítást, ha mindhárom teljesül.

A kiegyenlítés egyes iterációinál számított négyzetösszeg nem helyes, mert közben még nem teljesülnek a feltételek. Csak az utolsó után ciklus után számított négyzetösszeg a jó. Ezért a ciklusok számát sok esetben nem lehet előre megmondani. Ez függ a példa adataitól, általában ha ez ellentmondások kisebbek akkor a ciklusok száma is kevesebb lesz. Ezen kívül befolyásolja a ciklusok számát az előzetes közelítő mátrix felvétele, A átszámítandó pontok elhelyezkedése is befolyásoló probléma lehet.

A kényszerek felvételénél csak a kettős kényszerek felírásának van értelme, mert csak ebben az esetben ad jó eredményt. Az iterációk lefutása is ennél lett a legjobb.

A paraméterek kis változásainak meghatározásánál a kiegyenlítésnél kissé más a helyzet. Ekkor minden iterációnál olyan közelítő mátrixunk van, mely kielégíti a forgató mátrix ortogonalitási feltételeit. Ezek minden közelítésnél szabatosan teljesülnek. A feladat az, hogy ezek olyan értékét határozzuk meg, melyek a legjobb forgatásnak feleljenek meg. Ekkor a felállított matematikai modell közelítő. Ezért a matematikai modell csak kis változás esetén elfogadható. Kis elforgatás esetén is azonban a következő forgató mátrixot is a paramétereknek pillanatnyilag legjobb értékeiből a szigorú, közelítés nélküli képletekkel számítjuk. A kiegyenlítés után a így a javításokból számított négyzet összeg nem lesz helyes, mert ez csak a közelítő matematikai modellnek felel meg és nem jó a szabatos megoldásnak. A kiegyenlítés utáni javításokat valójában a következő kiegyenlítés javítási egyenleteinek tisztatagjai adják. A javítások négyzetösszegét is ebből kellene számítani. Ezért itt is, nem elegendő a kiegyenlítés javításainak négyzetösszegét figyelni.

Emellett a tisztatagok négyzetösszegét is figyelni kell, ez az iterációk során közelít a javítások négyzetösszegéhez. A meghatározott forgató mátrix végső kiegyenlítés után már nem változhat. Ezért ennek változása is ellenőrizendő. Többször tapasztaltuk, hogy a forgató mátrix még akkor is jelentősen változik amikor a másik két mennyiség már alig módosul.

A különböző közelítő forgatási paraméterek esetén nem azonos iterációt kaptunk. Tapasztalataink szerint leggyengébb az Euler szimmetrikus paramétereinél volt, általában. A ferdén szimmetrikus paramétereknél és a három tengely körüli közelítő forgatásnál ez már jobb volt. Legjobb közelítés a térbeli tengely körüli kis forgatásnál volt.

Egyes példáknál az iteráció szétesett, egy darabig szépen futott, de az egyik ciklus után a javítások négyzetösszege, és a többi figyelt szám értéke is romlani kezdett, olyannyira, hogy egy idő után már durva hibás volt a meghatározott forgató mátrix.

Ez több esetben elő fordult a *8H példánál, de tapasztaltuk a *27 példánál is. Ezeknél a várható javítások relatíve lényegesen kisebbek, mint a bemutatásra választott *8L példánál. A kiválasztott 8L példánál egyik megoldásnál sem tapasztaltunk ilyen eltorzulást.

A korábban említett példáknál azonban többször előfordult. Ilyen esetekben sokszor segített, ha a számított változások csak egy részét engedtük, meghatározott hányadát adtuk hozzá a paraméterek előzetes értékéhez. De ez sem csodaszer, nem minden estben eredményes.

Felmerül, hogy a kiegyenlítésnek a legjobb minimum helye mellett van más helyi minimuma is, és előfordulhat, hogy egy ilyen helyi minimumban áll meg a kiegyenlítés.

A közelítő kiegyenlítéseknél nem lehet előre megadni a szükséges ciklusok számát. Ez a ciklusok alakulásától függ. Csak akkor lehetünk nyugodtak az eredmény helyességében, ha minden figyelt mennyiség a ciklusok során szépen megállapodott.

A számpéldák során néhány ciklus lefutását is bemutatjuk. A ciklusszám jelentősen nagyobb, mint azt néhány esetben olvastuk. Ennek oka elsősorban abban van, hogy a bemutatott példánál viszonylag nagyok a hibák a gyakorlatban előforduló feladatokhoz képest, és a számítás eredményeinél is nagyobb élességet kívántunk meg.

6. Számpéldák a forgató mátrix meghatározására

6.1. A minta példák felvétele

A bemutatott kiegyenlítési eljárásokat számpéldával is vizsgáltuk. A példák során több különböző feladatot oldottunk meg. Ezek mind felvett számpéldák.

1. példa

Az első példa adatait egy téglatest sarokpontjaiként vettük fel. A téglatest oldal hosszai közelítően 800´500´200 egység hosszúak, mintegy 50 egységgel ingadoznak jelzett értékekhez. A második rendszer koordinátáit úgy kaptuk, hogy eredeti koordinátákat áttranszformáltuk és egész értékre kerekítettük.

	Első rendszer			Második rendszer
	Eredeti koordináták
pontszám	X	Y	Z	X	Y	Z
1	104	209	351	503	112	258
2	972	217	329	743	937	384
3	938	753	395	329	971	732
4	143	701	378	128	219	561
5	159	735	543	187	191	717
6	187	242	504	577	150	414
7	915	280	587	804	817	620
8	990	791	553	303	979	890
súlypont	551	491	455	458	547	572
	Súlyponti koordináták
	X	Y	Z	X	Y	Z
1	-447	-282	-104	+45	-435	-314
2	+421	-274	-126	+285	+390	+188
3	+387	+262	-60	-129	+424	+160
4	-408	+210	-77	-330	-328	-11
5	-392	+244	+88	-271	-356	+145
6	-364	-249	+49	+119	-397	-158
7	+364	+211	+132	+346	+270	+48
8	-439	+300	+98	-65	+432	+318
S	0	0	0	0	0	0

Példa neve: *8L

A példában az egyes koordináták javításai viszonylag nagyok, sok esetben 0,5-0,7 egységűek. Ez a néhány százegységű oldalhosszakhoz nagy. Azért választottunk ilyen nagy hibákat, hogy a különböző megoldások közötti eltérések határozottan észre vehetők legyenek.

2. példa

	Első rendszer			Második rendszer
pontszám	X	Y	Z	X	Y	Z
1	103	201	319	174,419	998,528	378,282
2	937	238	348	692,255	782,707	997,179
3	140	801	372	105,459	402,227	316,251
4	152	267	771	535,757	873,617	123,543
5	994	892	397	620,441	130,185	947,923
6	187	853	703	375,097	304,838	137,897
7	908	279	780	996,655	700,823	697,543
8	971	845	734	875,037	143,075	721,382

Példa neve: *8H

A példa pontjai közelítően egy téglalap sarok pontjai, a méretek 800´600´400 egységűek. A második rendszer pontjait három tizedes élességgel adtuk meg. Átszámítás után a pontok javításai 1-3×E-3 nagyságúak lesznek. Ezek a javítások már megfelelnek a geodéziai feladatok javításainak.

3. példa

	Első rendszer			Második rendszer
pontszám	X	Y	Z	X	Y	Z
1	124	238	429	359,2	485,5	079,3
2	153	308	491	391,7	437,7	158,4
3	101	570	413	249,7	209,7	231,0
4	151	247	703	609,4	454,5	190,3
5	138	371	794	660,4	335,0	273,5
6	175	579	791	589,5	191,3	411,5
7	147	200	934	841,1	456,3	234,1
8	159	314	982	85,3	365,5	318,4
9	179	535	972	772,1	202,4	447,7
10	458	285	422	281,5	644,7	366,4
11	413	374	401	243,1	550,7	371,0
12	491	505	481	266,1	480,3	526,7
13	471	273	703	547,0	621,4	457,4
14	481	397	708	513,2	527,7	532,2
15	473	532	718	483,9	413,9	600,0
16	408	205	934	794,9	605,2	443,4
17	419	348	978	792,0	491,4	541,1
18	487	583	979	711,7	343,8	718,8
19	842	205	419	236,7	934,2	627,2
20	831	315	490	272,7	829,8	698,5
21	815	591	428	135,4	609,5	811,9
22	874	207	782	571,7	898,8	766,3
23	892	371	778	516,4	779,4	865,7
24	874	509	711	415,7	668,4	903,2
25	818	281	948	715,4	783,1	812,5
26	851	308	918	673,7	785,3	843,5
27	870	528	998	680,5	609,5	999,0

Példa neve: *27

A példa pontjai egy téglatest sarokpontjai, ezt mindhárom irányba egy-egy síkkal elmetszettünk és a metszésvonal pontjait is megadtuk. A pontok mintegy 50 egységgel illeszkednek a szabályos téglatestre. A javítások várhatóan 0,2 egységnél kisebbek.

6.2. Kiegyenlítés kényszer feltételekkel

6.2.1. Merőlegességi kényszerek felírásával

Az 5.2 fejezetben leírtak alapján elvégeztük a kiegyenlítést. Az eredményeket az alábbi táblázatban foglaltuk össze.

feltételek	javítások			javítás hossza
XY YZ XZ	Y00; 0Z0; 00X
pontszám	X	Y	Z	D
1	+0,259 923 5	-0,196 817 0	-0,172 356 8	0,368 787 3
2	-0,844 095 5	+0,015 836 4	+0,021093 5	0,844 507 5
3	+0,132 494 9	+0,050 769 0	-0,040 281 9	0,147 495 9
4	+0,060 263 3	+0,103 966 9	+0,185 116 9	0,220 701 3
5	+0,781 793 6	-0,246 543 2	-0,037 282 7	0,820 009 0
6	+0,576 321 8	-0,058 146 3	+0,063 179 6	0,582 719 9
7	-0,694 071 4	+0,017 668 6	-0,090 979 1	0,700 231 7
8	-0,272 016 3	+0,313 634 0	+0,071 510 4	0,421 275 3
Svv	2,599 435 5
	+0,295 419 9	+0,941 730 6	+0,160 843 4
R=	-0,813 508 4	+0,159 688 1	+0,559 199 2
	+0,500 930 2	-0,296 046 0	+0,813 280 8

A kiegyenlítés során az iteráció alakulását a javítások négyzetösszegének változása mellett, még a forgató mátrix elemeinek változását és a forgató mátrix ortogonalitásának alakulását is célszerű figyelni. Alkalmanként megfigyelhető volt, hogy a javítások négyzetösszege kis mértékben emelkedett az ortogonalitási feltételek teljesülése közben. A különböző példák esetében gyorsan bekövetkező eredményeket kaptunk.

Nézzünk egy másik kényszer felírási lehetőséget

	Javítások			javítás hossza
XY YZ XZ	0X0; 0Z0; Z00
pontszám	X	Y	Z
1	+0,148 916 0	-0,260 565 3	-0,142 675 6	0,332 304 9
2	-0,379 198 6	-0,303 193 4	+0,062 780 1	0,489 550 0
3	+0,561 641 9	+0,198 571 4	-0,087 022 3	0,602 034 2
4	-0,295 035 5	+0,463 661 9	+0,130 930 2	0,564 952 1
5	+0,362 163 3	-0,055 257 2	-0,077 602 7	0,374 483 1
6	+0,176 207 3	-0,196 101 2	+0,106 716 8	0,284 417 2
7	-0,409 732 2	-0,357 031 6	+0,030 881 5	0,544 339 6
8	-0,132 870 1	+0,399 401 0	+0,037 754 8	0,422 612 2
Svv	1,727 739 4
	+0,296 413 5	+0,941 415 2	+0,160 861 9
R=	-0,813 451 3	+0,160 601 6	+0,559 020 7
	+0,500 435 9	-0,296 554 6	+0,813 399 8

A két megoldás eltér egymástól. A kényszerek felírásától függ a meghatározott forgató mátrix. Jelentős eltéréseket tapasztaltunk a javítások négyzetösszegében és forgató mátrix elemeiben is a különböző kényszereknél.

Kilenc kényszer felírásával

Nézzük meg a kényszerek egyértelmű felírását. Először vegyük a kilenc kényszernek megfelelő esetet, amikor a merőlegességi kényszereket kétszer írjuk fel:

Kilenc kényszer	Javítások			javítás hossza
XY YZ XZ	0X0; Y00; 0Z0; 00Y Z00; 00X
pontszám	X	Y	Z
1	+0,207 276 3	-0,207 592 0	-0,165 010 8	0,336 580 6
2	-0,542 506 1	-0,122 384 9	+0,190 576 8	0,587 886 5
3	+0,263 042 6	+0,110 437 1	-0,093 361 8	0,300 173 6
4	-0,101 742 6	+0,273 449 0	-0,006 692 3	0,291 840 2
5	+0,520 199 7	-0,113 774 5	-0,197 868 6	0,568 070 7
6	+0,458 506 6	-0,113 506 3	+0,112 292 2	0,485 511 6
7	-0,581 822 7	-0,161 135 7	+0,106 861 5	0,613 108 3
8	-0,222 953 8	+0,334 507 4	+0,053 203 2	0,405 504 8
Svv	1,732 933 7
	+0,295 815 1	+0,941 572 8	+0,161 040 7
R	-0,813 729 5	+0,160 082 8	+0,558 764 5
	+0,500 337 6	-0,296 334 6	+0,813 540 5

A kilenc kényszer felírásakor nagyobbak a javítások négyzetösszege, mint az egyik bemutatott előző esetben. Ezt más példák esetében is tapasztaltuk. A forgató mátrix elemei változtak

6.2.2. Kettős merőlegességi kényszer felírásával

Nézzük a másik megoldást, amikor a kényszerek egyértelmű felírására, ekkor minden kényszerben kétszer írtuk be a feltételt, így egy szorzat egyszer úgy szerepel, hogy az egyik tényezője paraméter, majd a második felírásnál a másik tényező lesz paraméter, ez tulajdonképpen a kényszer kettős felírását jelenti:

	javítások			javítás hossza
	YX0; 0ZY Z0X Kettős kényszerek			XY YZ XZ
	X	Y	Z
1	+0.01902453652412	-0.20172130135711	-0.20017378435006	+0.28482092681576
2	-0.43460089933728	-0.20621888787321	+0.18002810938347	+0.51362855410172
3	+0.42757661162454	+0.14329272008393	-0.04813478860100	+0.45351022073493
4	-0.21429183367650	+0.38615990908687	+0.01395204501883	+0.44185418966739
5	+0.41817957098471	-0.03178399729870	-0.18685406006466	+0.45912832175317
6	+0.30339035662921	-0.14335297196607	+0.07008440577775	+0.34279382579084
7	-0.48410635086077	-0.28153826311114	+0.08033521225848	+0.56575303699405
8	-0.03517199188801	0.33516279243543	+0.09076286057723	+0.34901155182407
Svv	1.51603588218931
	+0.29615521768158	+0.94146156021345	+0.16106587993871
R=	-0.81360287185407	+0.16032108767828	+0.55888059167989
	+0.50034233675633	-0.29655906576280	+0.81345575575019
	1 304 660	76 298	40 376
N=		523 402	42 781
			73 394
	+344912	+1228535	+285364	oszlopok szerint
n=	-382139	+142637	+339664
	+13845	+23111	+90109

Ciklus szám	Az iterációk lefutása
	Javítások négyzet összege	Eltérés az előzőtől	A forgató mátrix változása	A merőlegességi feltétel teljesülése
1	3.76512471609177	-3.76512471609177	+0.00170282389996	+0.00135374249955
2	1.51652147623289	2.24860323985888	+0.00000103355468	+0.00000112895915
3	1.51603588235563	+0.00048559387726	+0.00000011986121	+0.00000000000040
4	1.51603588218931	+0.00000000016632	+0.00000005990536	+0.00000000000000
5	1.51603588218937	-0.00000000000006	+0.00000002994006	+0.00000000000000
6	1.51603588218924	+0.00000000000012	+0.00000001496373	+0.00000000000000
7	1.51603588218917	+0.00000000000007	+0.00000000747872	+0.00000000000000
8	1.51603588218951	-0.00000000000034	+0.00000000373779	+0.00000000000000
9	1.51603588218920	+0.00000000000030	+0.00000000186811	+0.00000000000000
10	1.51603588218948	-0.00000000000027	+0.00000000093366	+0.00000000000000
15	1.51603588218920	+0.00000000000012	+0.00000000002912	+0.00000000000000
20	1.51603588218922	+0.00000000000016	+0.00000000000091	+0.00000000000000
25	1.51603588218930	+0.00000000000001	+0.00000000000003	+0.00000000000000
30	1.51603588218934	+0.00000000000002	+0.00000000000000	+0.00000000000000
35	1.51603588218932	+0.00000000000001	+0.00000000000000	+0.00000000000000
40	1.51603588218931	-0.00000000000002	+0.00000000000000	+0.00000000000000
45	1.51603588218929	+0.00000000000002	+0.00000000000000	+0.00000000000000
50	1.51603588218931	-0.00000000000002	+0.00000000000000	+0.00000000000000

A ciklusok lefutása mutatja, hogy a javítások négyzetösszege már 5 ciklus után beáll a véglegest jól megközelítő értékre., azonban még az 50-dik ciklusban is mutat egy kis ingadozást. A forgató mátrix azonban még változik és csak a 20-25-dik ciklus után nyugszik meg. A mátrix merőlegességi feltétele is igen hamar teljesül, a 4-5-dik ciklusra.

Több példa megoldásánál is azt tapasztaltuk, hogy a kettős kényszerek felírásakor kapjuk a legkisebb értéket a javítások négyzet összegére. Az iterációk lefutása is kedvező volt.

6.3. Kiegyenlítés a forgató mátrix inverzének kényszere alapján

pont száma	Javítások			Hossza
	X	Y	Z	D
1	+0,207 276 3	-0,207 592 0	-0,165 101 8	0,336 58 6
2	+0,542 506 1	+0,122 384 9	+0,190 576 8	0,587 886 5
3	+0,263 042 6	+0,110 437 1	-0,093 361 8	0,300 173 6
4	-0,101 742 6	+0,273 449 0	-0,006 692 2	0,291 840 2
5	+0,520 199 7	-0,113 774 5	-0,197 868 6	0,568 070 7
6	+0,458 506 6	-0,113 506 3	+0,112 292 2	0,485 511 6
7	-0,581 822 7	-0,161 135 7	+0,106 861 5	0,613 108 3
8	-0,222 953 8	+0,334 507 4	+0,053 203 2	0,405 504 8
Svv	1,285 881 5	-0,067 462 2	-0,286 949 9
		+0,308 731 4	+0,009 134 8
			+0,138 320 8	1,732 933 7
	+0,295 815 1	+0,941 572 8	+0,161 040 7
R	-0,813 729 5	+0,160 082 8	+0,558 764 5
	+0,500 337 6	-0,296 334 6	+0,813 540 5

Az eredmény teljesen azonos, mint a kilenc kényszer felírásakor. Az iteráció nagyon gyorsan megtörtént még ilyen viszonylag nagy javítások esetén is.

6.4. Kis szögekkel végzett forgatás

pontszám	javítások			hossza
	X	Y	Z	d
1	+0.01902453652414	-0.20172130135706	-0.20017378435004	+0.28482092681571
2	-0.43460089933730	-0.20621888787330	+0.18002810938346	+0.51362855410177
3	+0.42757661162453	+0.14329272008387	-0.04813478860102	+0.45351022073489
4	-0.21429183367653	+0.38615990908690	+0.01395204501883	+0.44185418966743
5	+0.41817957098472	-0.03178399729861	-0.18685406006468	+0.45912832175319
6	+0.30339035662924	-0.14335297196600	+0.07008440577777	+0.34279382579085
7	-0.48410635086074	-0.28153826311117	+0.08033521225848	+0.56575303699403
8	-0.03517199188804	+0.33516279243531	+0.09076286057716	+0.34901155182394
Svv	+1.51603588218926
	+0.29615521768158	+0.94146156021345	+0.16106587993871
R	-0.81360287185407	+0.16032108767828	+0.55888059167989
	+0.50034233675633	-0.29655906576280	+0.81345575575019
	E+6			E-9
	+1.48182084761984	-0.25900931055888	+0.14662964598678	+0.00716226383757
N ïn		+0.72874469338951	+0.29662380091371	-0.07967673482795
			+1.59234645899065	+0.14855315068341
	E-5			Paraméterek az utolsó iteráció után E-16
	+0.07201443592144	-0.02477453475078	-0.00201635426972	-0.17577034253011
Q		+0.15700343104169	+0.02696540879634	-0.83262825516869
			+0.06800921919452	+0.79400263994016

Az eredmény teljesen egyezik a kettős kényszerek felírásakor kapott eredményekkel. Több példa alapján ez a megoldás gyakran vezet gyenge eredményre. Az iteráció egy darabig szépen folyik, de egy pontnál emelkedni kezd a javítások négyzetösszege és a kiegyenlítés eltorzul. Ilyen jelenséget a pontosabban felírt mintapéldánál is tapasztaltunk. Nagyon gyengén

konvergált a 2 példa is pedig a várható javítások jelentősen kisebbek, mint a bemutatott példánál. Ezeknél olyat is tapasztaltunk, hogy a iteráció folyamatosan gyengébb eredményeket ad, a javítások négyzetösszege rendszeresen emelkedik, majd csökkeni kezd. Az iteráció lefutása több esetben más eredmény adott, ha az előzetes értékeket máshogy vettük fel előfordult, hogy az eredmény nagyon lassan konvergált egy értékhez, de nem vált véglegessé, egy érték körül ingadozott.

Az iteráció alakulása (B8L.M példa)
	Javítások négyzetösszege	Eltérés az előzőtől	A tisztatagok négyzetösszegének eltérése	A forgató mátrix eltérése az előző mátrixtól
1	1.51609138164660	-1.51609138164660	0.68395366590085	0.00139687091205
2	1.51602877777639	0.00006260387021	0.03346452835670	0.00067221389479
3	1.51603551714146	-0.00000673936507	0.00238462022401	0.00014959961866
4	1.51603573347776	-0.00000021633630	0.00062926122170	0.00003005629738
5	1.51603587760274	-0.00000014412498	0.00002952008783	0.00001747369195
6	1.51603588103046	-0.00000000342772	0.00000557422713	0.00000405592063
7	1.51603588201037	-0.00000000097991	0.00000078150612	0.00000135825763
8	1.51603588218522	-0.00000000017485	0.00000003414900	0.00000069561671
9	1.51603588218686	-0.00000000000165	0.00000001079085	0.00000012074723
10	1.51603588218924	-0.00000000000238	0.00000000075332	0.00000006639632
11	1.51603588218925	-0.00000000000001	0.00000000007303	0.00000002244171
12	1.51603588218934	-0.00000000000009	0.00000000001604	0.00000000489316
13	1.51603588218918	0.00000000000017	0.00000000000067	0.00000000292704
14	1.51603588218930	-0.00000000000012	0.00000000000016	0.00000000055223
15	1.51603588218937	-0.00000000000008	0.00000000000002	0.00000000024524
16	1.51603588218934	0.00000000000003	0.00000000000000	0.00000000010899
17	1.51603588218927	0.00000000000007	0.00000000000000	0.00000000001989
18	1.51603588218926	0.00000000000001	0	0.00000000001119
19	1.51603588218926	0.00000000000000	0	0.00000000000325
20	1.51603588218925	0.00000000000001	0	0.00000000000079
21	1.51603588218922	0.00000000000003	0.00000000000000	0.00000000000048
22	1.51603588218927	-0.00000000000005	0	0.00000000000009
23	1.51603588218936	-0.00000000000009	0	0.00000000000004
24	1.51603588218928	0.00000000000007	0	0.00000000000002
25	1.51603588218925	0.00000000000003	0.00000000000000	0.00000000000000
26	1.51603588218926	-0.00000000000001	0.00000000000000	0.00000000000000
27	1.51603588218919	0.00000000000007	0	0.00000000000000
28	1.51603588218926	-0.00000000000007	0	0.00000000000000
29	1.51603588218921	0.00000000000004	0	0.00000000000000
30	1.51603588218926	-0.00000000000004	0	0.00000000000000

A második és harmadik oszlopban a javítások négyzetösszegétől számított eltérések szerepelnek. A táblázatból láthatjuk, hogy a javítások négyzetösszege viszonylag gyorsan csökken, és ezt lassabban követi a tisztatagok négyzetösszegének csökkenése, még lassabban változik a forgató mátrix elemeinek beállása. Azt is láthatjuk, hogy az iteráció szépen, folyamatosan alakul és jelentősebb ingadozás nélkül beáll a végső helyzetbe. Ebben az esetben is a Svv a kezdetben kis mértékben nő és csak később csökken.

A ferdén szimmetrikus paraméterek változásának meghatározása kiegyenlítéssel

Az eredmény azonos a három tengely körüli kis szögekkel végzett, előző pontban ismertetett számítással.

Transzformációs mátrix

+0.29615521768158	+0.94146156021345	+0.16106587993871
-0.81360287185407	+0.16032108767828	+0.55888059167989
+0.50034233675633	-0.29655906576280	+0.81345575575019

paraméterek

e=+0.37685694303307

f=+0.14946546754871

g=+0.77317927797771

Normál egyenlet rendszer együttható mátrirsza N E+6

+1.48182084761984	-0.25900931055888	+0.14662964598678
-0.25900931055888	+0.72874469338951	-0.29662380091371
+0.14662964598678	-0.29662380091371	+1.59234645899065

A súlykoefficiens mátrix Q E-5

+0.07201443592144	+0.02477453475078	-0.00201635426972
+0.02477453475078	+0.15700343104169	+0.02696540879634
-0.00201635426972	+0.02696540879634	+0.06800921919452

javítások

Vx	Vy	Vz	hossza
+0.01902453652415	-0.20172130135706	-0.20017378435005	+0.28482092681572
-0.43460089933730	-0.20621888787326	+0.18002810938346	+0.51362855410175
+0.42757661162450	+0.14329272008393	-0.04813478860101	+0.45351022073489
-0.21429183367654	+0.38615990908692	+0.01395204501884	+0.44185418966745
+0.41817957098466	-0.03178399729865	-0.18685406006465	+0.45912832175312
+0.30339035662926	-0.14335297196601	+0.07008440577776	+0.34279382579087
-0.48410635086072	-0.28153826311119	+0.08033521225847	+0.56575303699402
-0.03517199188805	+0.33516279243537	+0.09076286057722	+0.34901155182402

A paraméterek alakulása az iterációk során: (csak minden ötödik eredmény jelezve)

	e	f	g
1	+0.37676522477341	+0.14949398697142	+0.77364578068435
5	-0.00002163597588	-0.00012668463165	-0.00000414770042
10	+0.00001248887811	+0.00000437491972	-0.00000753477032
15	-0.00000125137936	+0.00000134879384	+0.00000034076154
20	-0.00000005975224	-0.00000021062299	+0.00000006979174
25	+0.00000002517780	+0.00000000194121	-0.00000001266623
30	-0.00000000176835	+0.00000000297482	+0.00000000028730
35	-0.00000000019275	-0.00000000034478	+0.00000000016080
40	+0.00000000004715	-0.00000000000837	-0.00000000002139
45	-0.00000000000209	+0.00000000000609	-0.00000000000016
50	-0.00000000000049	-0.00000000000052	+0.00000000000034
55	+0.00000000000008	-0.00000000000004	-0.00000000000003
60	+0.00000000000000	+0.00000000000001	+0.00000000000000
61	+0.00000000000000	+0.00000000000001	+0.00000000000000
62	+0.00000000000000	+0.00000000000000	+0.00000000000000

Az Euler paraméterek kis változásainak meghatározása iterációval

Az eredmény azonos a három tengely körüli kis szögekkel végzett, előző pontban ismertetett számítással.

Térbeli tengely körüli elemi forgatás kiegyenlítése

Az eredmény azonos a három tengely körüli kis szögekkel végzett, 6.4 pontban ismertetett számítással.

A kiegyenlítés lefutása (E8L.M)
	Javítások négyzetösszege	Eltérés az előzőtől	Tisztatagok négyzetösszegének eltérése	Elfordulási szög
1	1.51604617865030	0.42449578412799	-0.42449578412799	1.43571789742617
2	1.51603588219517	0.00001029645513	-0.00000002936739	0.00052924875264
3	1.51603588218931	0.00000000000587	0.00000000000000	0.00000016340352
4	1.51603588218941	-0.00000000000011	0.00000000000000	0.00000000004811
5	1.51603588218941	0.00000000000000	0	0.00000000000002
6	1.51603588218932	0.00000000000009	0	0.00000000000000
7	1.51603588218931	0.00000000000002	0	0.00000000000000
8	1.51603588218928	0.00000000000002	0	0.00000000000000
9	1.51603588218925	0.00000000000004	0	0.00000000000000
10	1.51603588218923	0.00000000000002	0	0.00000000000000
11	1.51603588218923	0	0	0.00000000000000
12	1.51603588218923	0	0	0.00000000000000

A feladat lefutásából látjuk, hogy milyen szépen iterált a megoldás felé. Ha összehasonlítjuk a három tengely körüli közelítő forgatás lefutásával akkor jelentős különbséget láthatunk. Az csak 25-30 ciklus után állt be a végleges értékre. Itt a hatodik ciklus után már beállt a megoldás és tovább már nem változott. A többi példánál is hasonlót tapasztaltunk ennek a megoldásnak a javára.

Hivatkozások

Euler, Leonhard :Problema algebraicum ob affectiones prorsus singulares memorabile ( L. Euleri Opera Omnia Series I.) Teubner, Leipzig/Bern, 1921, Volumen VI. 287-315

Euler, Leonhard : Demonstratio theorematis Fermatiani omnem numerum sive integrum …(L. Euleri Opera Omnia, Series I.) Teubner, Leipzig, 1915, Volume II. 338-372

Detrekői Ákos (1991): Kiegyenlítő számítások. Tankönyvkiadó, Budapest

Fazekas Ferenc (1972): Márixszámítás, Müszaki Matematikai Gyakorlatok, C.IV. Tankönyvkiadó, Budapest

Gellert, W. - Küstner, H - Hellwich, M. - Kästner, H. (1985): Kleine Enziklopädie Mathematik. VEB Bibliographisches Institut Leipzig

Korn, G. A. Korn, T. M. (1975): Matematikai kézikönyv műszakiaknak, Műszaki könyvkiadó, Budapest

Mirski, L (1955): An Introduction to Linear Algebra, Clanderon Press, Oxford, Ch. VIII.

Rinner, Karl (1957): Über räumliche Drehungen. Deutsche Geodätische Kommission Reiche A, Heft 25. München Verlag der Bayerischen Akademie der Wissenschaften

Rózsa Pál (1974): Lineáris algebra és alkalmazásai. Műszaki Könyvkiadó, Budapest.

Schut, G. H. (1958): Construction of Ortogonal Matrices and their Application In Analitical Photogrammetry, Photogrammetria XV Nr. 4.

Sain Márton (1986): Nincs királyi út! Matemetika történet. Gondolat kiadó, Budapest

Somogyi József (1969): A forgatási mátrix elemeinek meghatározása közvetlen úton. Geodézia és Kartográfia 264-267.

Ugrin Nándor (1978): A fotogrammetria geometriai alapjai. Budapesti Műszaki Egyetem, egyetemi jegyzet

Zhizhuo, Wang (1990) : Principles of Photogrammetry. Press of Wuhan Technikal University of Surveying and Mapping, Publishing House of Surveying and Mapping, Beijing